在机器学习领域中,正则化(Regulization)是一种用来解决过拟合的方法。
如果不知道什么是过拟合,可以参考 过拟合 。
思想:在损失函数后面加上系数向量的二范数,约束系数向量的增长。
正则化原理
假设原始损失函数为:
\[ \boldsymbol{J} = [\boldsymbol{y}_{\theta}(\boldsymbol{x}) - \boldsymbol{y}]^2 \]
那么,正则化之后的损失函数可以是
\[ \boldsymbol{J} = [\boldsymbol{y}_{\boldsymbol{\theta}}(\boldsymbol{x}) - \boldsymbol{y}]^2 + \lambda \boldsymbol{\theta}^T \boldsymbol{\theta} \]
其中, \( \lambda \) 是一个需要手调的参数。
为什么正则化可以解决过拟合问题?
首先正则化的含义是同时约束误差项和模型系数的范数,不能让范数不受控制的增长。
那么为题就转变为:为什么约束范数的增长可以解决过拟合问题?
首先要达到过拟合的效果,光有高阶模型还不够,高阶模型的系数还要足够大,才能够拟合曲曲折折的高阶函数,如果对系数进行范数进行约束,那么拟合后的函数更光滑,限制某些参数对数据中“外点”的拟合。
那么为什么系数大,函数就不光滑呢?这是因为系数决定这输出对输入的敏感度,如果系数越大,那么只要x一小点,y都能有很大的变化,这实际上就是一种不平滑。
注意, \( \boldsymbol{\theta} \)只考虑自变量 \( x \)的系数参数,bias项不考虑。
L1范数正则化和L2范数正则化
上一节的例子实际上是L2正则化,L1正则化实际上限制的是系数向量的L1范数,也就是绝对之和。
我们知道限制范数,也就是限制向量的扩张区间,两者有什么区别呢?
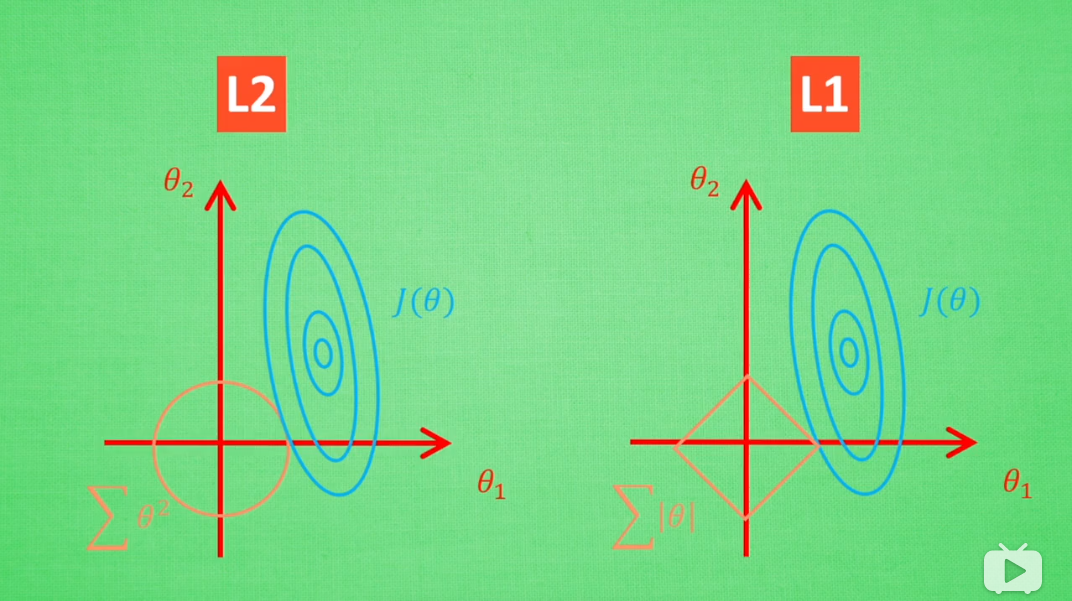
有一些讲的非常棒的视频:
